This tool is based on the paper Temporal Behavior Trees: Robustness and Segmentation and its companion poster Temporal Behavior Trees - Segmentation, which were published at HSCC'24.

If you encounter any issues, have questions, or need assistance, feel free to reach out: sebastian dot schirmer at dlr dot de

Temporal Behavior Trees: Robustness and Segmentation

Temporal Behavior Trees (TBT) are a specification formalism for monitoring behaviors.
They are inspired by behavior trees that are commonly used to program robotic applications, but allow to specify temporal properties in their leaf nodes.
Therefore, they can be easily retrofitted to existing behavior trees.

For instance, consider the following behavior tree that specifies the landing sequence of an unmanned aircraft (1) move to position, (2) stay in position, (3) move to touchdown, and (4) descend:

Given such a TBT specification and a trace, i.e., a sequence of events of a system, we can compute the corresponding robustness.
Robustness provides an quantitative interpretation how much the TBT specification was satisfied or violated.

Further, we can use a TBT specification to segment a trace.
That means that we assign portions of the provided specification to segments of the given trace.
Such a segmentation then helps to better explain which portions of the specification were satisfied or violated.

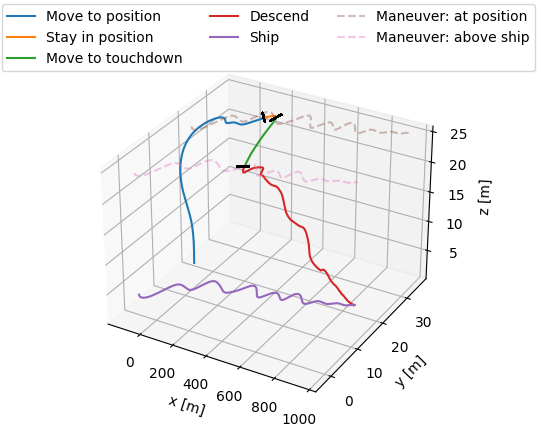
It is also useful to visualize the resulting segmentation, as shown below for the landing maneuver:

Getting Started

Requires Rust to compile source code and Python for visualization.

1. Install Rust
2. Specify a TBT, e.g., as done here. The grammar can be found here
3. Provide a Trace by implementing get_trace
4. Replace the user_defined-function by your own (Line 5)
5. Call cargo build or cargo build --release
6. Call cargo run -- --help to get help on the command-line-usage
7. Call cargo test to see if the tests are successful

For instance:

cargo run --release -- -u -s specification/shiplanding_formula_combined.tbt -f ./res/logs_wind_front_Lateral/ runs segmentation using subsampling on a provided logfile.
For this example, get_trace is already provided.

Using the visualization script, we can easily plot a segmentation by, e.g., python visualize_ship_landing.py plot -b Lateral -s 5000 10000 20000 -e 0 -l ../res/logs_wind_front_Lateral/ where 5000, 10000, 20000 represent beginning of segments (omitting 0), -b states the expected behavior and is used to plot the dotted lines, and -e represents the number of skipped entries due to subsampling. There is also the option to save a plot to inspect it in a docker environment using -p.
We can also replay the flight by, e.g., python visualize_ship_landing.py live -l ../res/logs_wind_front_Lateral/ -b Lateral -f 0.005 0.1 2.0.

For more information call python visualize_ship_landing.py --help.

Using --toml <FILE> as command-line-argument generates a .toml-file for the computed segmentations.

Brief Summary of the Supported Operators

TBT T:=

• Fallback([T_1,...,T_n]): At least one of the subtrees must eventually be satisfied.
• Sequence([T_1, T_2]): Each subtree must be satisfied in order from left to right.
• Parallel(m, [T_1,...,T_n]): At least m of the subtrees must be simultaneously satisfied.
• Timeout(t, T): The subtree must be satisfied by a finite prefix of length t.
• Kleene(n, T): There must be n repetitions of the subtree to be satisfied.
• Leaf(S): STL formula S must be satisfied.

STL S:=

• Atomic(function): The function must return a positive number to be satisfied, otherwise it is violated.
• Conjuntion(S_1, S_2): Both subformulas must be satisfied.
• Disjunction(S_1, S_2): One of the subformulas or both must be satisfied.
• Neg(S): The subformulas must be violated.
• Next(S): The subformula must be satisfied in the next step.
• Eventually(S): Eventually the subformula must be satisfied.
• Globally(S): The subformula must always be satisfied.
• Until(S_1, S_2): The subformula S_1 must be satisfied until S_2 is satisfied.
• EventuallyInterval(l, u, S): Eventually within l and u steps, the subformula must be satisfied.
• GloballyInterval(l, u, S): Always within l and u steps, the subformula must be satisfied.
• UntilInterval(l, u, S_1, S_2): Within l and u steps, the subformula S_1 must be satisfied until S_2 is satisfied.

The TBT operators are defined here and the STL operators are defined here.

A TBT parser is implemented that is based on this grammar.

For more details, we refer to the paper.