Millepede II

In certain least squares fit problems with a very large number of parameters, the set of parameters can be divided into two classes: Global and local parameters. Local parameters are only relevant in subsets of the data. Contrary, detector alignment and calibration based on track fits are amongst the problems where the interest is in optimal values of the global parameters, the alignment parameters.

The method, called Millepede, to solve the linear least squares problem with a simultaneous fit of all global and local parameters, irrespectively of the number of local parameters, has been developed as experiment-independent programs by Prof. V. Blobel (Univ. Hamburg).

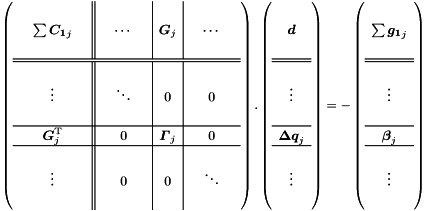The complete linear equation system with a (huge) bordered band matrix.

The current Millepede II version consists of two parts: "mille" and "pede". The mille step has to be integrated in the experiment specific tracking software to produce dedicated binary files containing all the information needed to build the linear equation system described the (linearised) alignment problem.

The standalone "pede" executable is then used to build and solve that equation system.

It has been highly optimised by exploring multiple threading with OpenMP and dedicated linear algebra libraries (LAPACK).